Hierarchical optimization with relative data

In this notebook we illustrate how to do hierarchical optimization in pyPESTO.

A frequent problem occuring in parameter estimation for dynamical systems is that the objective function takes a form

\[J(\theta, s, b, \sigma^2) = \sum_i \left[\log(2\pi\sigma_i^2) + \frac{(\bar y_i - (s_iy_i(\theta) + b_i))^2}{\sigma_i^2}\right]\]

with data \(\bar y_i\), parameters \(\eta = (\theta,s,b,\sigma^2)\), and ODE simulations \(y(\theta)\). Here, we consider a Gaussian noise model, but also others (e.g. Laplace) are possible. Here we want to leverage that the parameter vector \(\eta\) can be split into “dynamic” parameters \(\theta\) that are required for simulating the ODE, and “static” parameters \(s,b,\sigma^2\) that are only required to scale the simulations and formulate the objective function. As simulating the ODE usually dominates the computational complexity, one can exploit this separation of parameters by formulating an outer optimization problem in which \(\theta\) is optimized, and an inner optimization problem in which \(s,b,\sigma^2\) are optimized conditioned on \(\theta\). This approach has shown to have superior performance to the classic approach of jointly optimizing \(\eta\).

In pyPESTO, we have implemented the algorithms developed in Loos et al.; Hierarchical optimization for the efficient parametrization of ODE models; Bioinformatics 2018 (covering Gaussian and Laplace noise models with gradients computed via forward sensitivity analysis) and Schmiester et al.; Efficient parameterization of large-scale dynamic models based on relative measurements; Bioinformatics 2019 (extending to offset parameters and adjoint sensitivity analysis).

However, the current implementation only supports: - Gaussian (normal) noise distributions - unbounded inner noise parameters \(\sigma\) - linearly-scaled inner parameters \(\eta\)

Scaling \(s\) and offset \(b\) parameters can be bounded arbitrarily.

In the following we will demonstrate how to use hierarchical optimization, and we will compare optimization results for the following scenarios:

Standard non-hierarchical gradient-based optimization with adjoint sensitivity analysis
Hierarchical gradient-based optimization with analytical inner solver and adjoint sensitivity analysis
Hierarchical gradient-based optimization with analytical inner solver and forward sensitivity analysis
Hierarchical gradient-based optimization with numerical inner solver and adjoint sensitivity analysis

[1]:

import time

import amici
import fides
import matplotlib.pyplot as plt
import numpy as np
from matplotlib.colors import to_rgba

import pypesto
from pypesto.hierarchical.relative import (
    AnalyticalInnerSolver,
    NumericalInnerSolver,
)
from pypesto.optimize.options import OptimizeOptions
from pypesto.petab import PetabImporter

Note on inclusion of additional data types:

It is possible to include observables with different types of data to the same petab_problem. Refer to the notebooks on using semiquantitative data, ordinal data and censored data for details on integration of other data types.

Problem specification

We consider a version of the [Boehm et al.; Journal of Proeome Research 2014] model, modified to include scalings \(s\), offsets \(b\), and noise parameters \(\sigma^2\).

NB: We load two PEtab problems here, because the employed standard and hierarchical optimization methods have different expectations for parameter bounds. The difference between the two PEtab problems is that the corrected_bounds version estimates inner noise parameters (\(\sigma\)) in \([0, \infty]\).

[2]:

# get the PEtab problem
# requires installation of
from pypesto.testing.examples import (
    get_Boehm_JProteomeRes2014_hierarchical_petab,
    get_Boehm_JProteomeRes2014_hierarchical_petab_corrected_bounds,
)

petab_problem = get_Boehm_JProteomeRes2014_hierarchical_petab()
petab_problem_hierarchical = (
    get_Boehm_JProteomeRes2014_hierarchical_petab_corrected_bounds()
)

To convert a non-hierarchical PEtab model to a hierarchical one, the observable_df, the measurement_df and the parameter_df have to be changed accordingly. The PEtab observable table contains placeholders for scaling parameters \(s\) (observableParameter1_{pSTAT5A_rel,pSTAT5B_rel,rSTAT5A_rel}), offsets \(b\) (observableParameter2_{pSTAT5A_rel,pSTAT5B_rel,rSTAT5A_rel}), and noise parameters \(\sigma^2\) (noiseParameter1_{pSTAT5A_rel,pSTAT5B_rel,rSTAT5A_rel}) that are overridden by the {observable,noise}Parameters column in the measurement table.

N.B.: in general, the inner parameters can appear in observable formulae directly. For example, the first observable formula in this table could be changed from observableParameter2_pSTAT5A_rel + observableParameter1_pSTAT5A_rel * (100 * pApB + 200 * pApA * specC17) / (pApB + STAT5A * specC17 + 2 * pApA * specC17) to offset_pSTAT5A_rel + scaling_pSTAT5A_rel * (100 * pApB + 200 * pApA * specC17) / (pApB + STAT5A * specC17 + 2 * pApA * specC17).

Observable DF:

[3]:

from pandas import option_context

with option_context("display.max_colwidth", 400):
    display(petab_problem_hierarchical.observable_df)

	observableName	observableFormula	noiseFormula	observableTransformation	noiseDistribution
observableId
pSTAT5A_rel	NaN	observableParameter2_pSTAT5A_rel + observableParameter1_pSTAT5A_rel * (100 * pApB + 200 * pApA * specC17) / (pApB + STAT5A * specC17 + 2 * pApA * specC17)	noiseParameter1_pSTAT5A_rel	lin	normal
pSTAT5B_rel	NaN	observableParameter2_pSTAT5B_rel + observableParameter1_pSTAT5B_rel * -(100 * pApB - 200 * pBpB * (specC17 - 1)) / ((STAT5B * (specC17 - 1) - pApB) + 2 * pBpB * (specC17 - 1))	noiseParameter1_pSTAT5B_rel	lin	normal
rSTAT5A_rel	NaN	observableParameter2_rSTAT5A_rel + observableParameter1_rSTAT5A_rel * (100 * pApB + 100 * STAT5A * specC17 + 200 * pApA * specC17) / (2 * pApB + STAT5A * specC17 + 2 * pApA * specC17 - STAT5B * (specC17 - 1) - 2 * pBpB * (specC17 - 1))	noiseParameter1_rSTAT5A_rel	lin	normal

Measurement DF:

[4]:

from pandas import option_context

with option_context("display.max_colwidth", 400):
    display(petab_problem_hierarchical.measurement_df)

	observableId	preequilibrationConditionId	simulationConditionId	measurement	time	observableParameters	noiseParameters	datasetId
0	pSTAT5A_rel	NaN	model1_data1	7.901073	0.0	scaling_pSTAT5A_rel;offset_pSTAT5A_rel	sd_pSTAT5A_rel	model1_data1_pSTAT5A_rel
1	pSTAT5A_rel	NaN	model1_data1	66.363494	2.5	scaling_pSTAT5A_rel;offset_pSTAT5A_rel	sd_pSTAT5A_rel	model1_data1_pSTAT5A_rel
2	pSTAT5A_rel	NaN	model1_data1	81.171324	5.0	scaling_pSTAT5A_rel;offset_pSTAT5A_rel	sd_pSTAT5A_rel	model1_data1_pSTAT5A_rel
3	pSTAT5A_rel	NaN	model1_data1	94.730308	10.0	scaling_pSTAT5A_rel;offset_pSTAT5A_rel	sd_pSTAT5A_rel	model1_data1_pSTAT5A_rel
4	pSTAT5A_rel	NaN	model1_data1	95.116483	15.0	scaling_pSTAT5A_rel;offset_pSTAT5A_rel	sd_pSTAT5A_rel	model1_data1_pSTAT5A_rel
5	pSTAT5A_rel	NaN	model1_data1	91.441717	20.0	scaling_pSTAT5A_rel;offset_pSTAT5A_rel	sd_pSTAT5A_rel	model1_data1_pSTAT5A_rel
6	pSTAT5A_rel	NaN	model1_data1	91.257099	30.0	scaling_pSTAT5A_rel;offset_pSTAT5A_rel	sd_pSTAT5A_rel	model1_data1_pSTAT5A_rel
7	pSTAT5A_rel	NaN	model1_data1	93.672298	40.0	scaling_pSTAT5A_rel;offset_pSTAT5A_rel	sd_pSTAT5A_rel	model1_data1_pSTAT5A_rel
8	pSTAT5A_rel	NaN	model1_data1	88.754233	50.0	scaling_pSTAT5A_rel;offset_pSTAT5A_rel	sd_pSTAT5A_rel	model1_data1_pSTAT5A_rel
9	pSTAT5A_rel	NaN	model1_data1	85.269703	60.0	scaling_pSTAT5A_rel;offset_pSTAT5A_rel	sd_pSTAT5A_rel	model1_data1_pSTAT5A_rel
10	pSTAT5A_rel	NaN	model1_data1	81.132395	80.0	scaling_pSTAT5A_rel;offset_pSTAT5A_rel	sd_pSTAT5A_rel	model1_data1_pSTAT5A_rel
11	pSTAT5A_rel	NaN	model1_data1	76.135928	100.0	scaling_pSTAT5A_rel;offset_pSTAT5A_rel	sd_pSTAT5A_rel	model1_data1_pSTAT5A_rel
12	pSTAT5A_rel	NaN	model1_data1	65.248059	120.0	scaling_pSTAT5A_rel;offset_pSTAT5A_rel	sd_pSTAT5A_rel	model1_data1_pSTAT5A_rel
13	pSTAT5A_rel	NaN	model1_data1	42.599659	160.0	scaling_pSTAT5A_rel;offset_pSTAT5A_rel	sd_pSTAT5A_rel	model1_data1_pSTAT5A_rel
14	pSTAT5A_rel	NaN	model1_data1	25.157798	200.0	scaling_pSTAT5A_rel;offset_pSTAT5A_rel	sd_pSTAT5A_rel	model1_data1_pSTAT5A_rel
15	pSTAT5A_rel	NaN	model1_data1	15.430182	240.0	scaling_pSTAT5A_rel;offset_pSTAT5A_rel	sd_pSTAT5A_rel	model1_data1_pSTAT5A_rel
16	pSTAT5B_rel	NaN	model1_data1	4.596533	0.0	scaling_pSTAT5B_rel;offset_pSTAT5B_rel	sd_pSTAT5B_rel	model1_data1_pSTAT5B_rel
17	pSTAT5B_rel	NaN	model1_data1	29.634546	2.5	scaling_pSTAT5B_rel;offset_pSTAT5B_rel	sd_pSTAT5B_rel	model1_data1_pSTAT5B_rel
18	pSTAT5B_rel	NaN	model1_data1	46.043806	5.0	scaling_pSTAT5B_rel;offset_pSTAT5B_rel	sd_pSTAT5B_rel	model1_data1_pSTAT5B_rel
19	pSTAT5B_rel	NaN	model1_data1	81.974734	10.0	scaling_pSTAT5B_rel;offset_pSTAT5B_rel	sd_pSTAT5B_rel	model1_data1_pSTAT5B_rel
20	pSTAT5B_rel	NaN	model1_data1	80.571609	15.0	scaling_pSTAT5B_rel;offset_pSTAT5B_rel	sd_pSTAT5B_rel	model1_data1_pSTAT5B_rel
21	pSTAT5B_rel	NaN	model1_data1	79.035720	20.0	scaling_pSTAT5B_rel;offset_pSTAT5B_rel	sd_pSTAT5B_rel	model1_data1_pSTAT5B_rel
22	pSTAT5B_rel	NaN	model1_data1	75.672380	30.0	scaling_pSTAT5B_rel;offset_pSTAT5B_rel	sd_pSTAT5B_rel	model1_data1_pSTAT5B_rel
23	pSTAT5B_rel	NaN	model1_data1	71.624720	40.0	scaling_pSTAT5B_rel;offset_pSTAT5B_rel	sd_pSTAT5B_rel	model1_data1_pSTAT5B_rel
24	pSTAT5B_rel	NaN	model1_data1	69.062863	50.0	scaling_pSTAT5B_rel;offset_pSTAT5B_rel	sd_pSTAT5B_rel	model1_data1_pSTAT5B_rel
25	pSTAT5B_rel	NaN	model1_data1	67.147384	60.0	scaling_pSTAT5B_rel;offset_pSTAT5B_rel	sd_pSTAT5B_rel	model1_data1_pSTAT5B_rel
26	pSTAT5B_rel	NaN	model1_data1	60.899476	80.0	scaling_pSTAT5B_rel;offset_pSTAT5B_rel	sd_pSTAT5B_rel	model1_data1_pSTAT5B_rel
27	pSTAT5B_rel	NaN	model1_data1	54.809258	100.0	scaling_pSTAT5B_rel;offset_pSTAT5B_rel	sd_pSTAT5B_rel	model1_data1_pSTAT5B_rel
28	pSTAT5B_rel	NaN	model1_data1	43.981290	120.0	scaling_pSTAT5B_rel;offset_pSTAT5B_rel	sd_pSTAT5B_rel	model1_data1_pSTAT5B_rel
29	pSTAT5B_rel	NaN	model1_data1	29.771458	160.0	scaling_pSTAT5B_rel;offset_pSTAT5B_rel	sd_pSTAT5B_rel	model1_data1_pSTAT5B_rel
30	pSTAT5B_rel	NaN	model1_data1	20.089017	200.0	scaling_pSTAT5B_rel;offset_pSTAT5B_rel	sd_pSTAT5B_rel	model1_data1_pSTAT5B_rel
31	pSTAT5B_rel	NaN	model1_data1	10.961845	240.0	scaling_pSTAT5B_rel;offset_pSTAT5B_rel	sd_pSTAT5B_rel	model1_data1_pSTAT5B_rel
32	rSTAT5A_rel	NaN	model1_data1	14.723168	0.0	scaling_rSTAT5A_rel;offset_rSTAT5A_rel	sd_rSTAT5A_rel	model1_data1_rSTAT5A_rel
33	rSTAT5A_rel	NaN	model1_data1	33.762342	2.5	scaling_rSTAT5A_rel;offset_rSTAT5A_rel	sd_rSTAT5A_rel	model1_data1_rSTAT5A_rel
34	rSTAT5A_rel	NaN	model1_data1	36.799851	5.0	scaling_rSTAT5A_rel;offset_rSTAT5A_rel	sd_rSTAT5A_rel	model1_data1_rSTAT5A_rel
35	rSTAT5A_rel	NaN	model1_data1	49.717602	10.0	scaling_rSTAT5A_rel;offset_rSTAT5A_rel	sd_rSTAT5A_rel	model1_data1_rSTAT5A_rel
36	rSTAT5A_rel	NaN	model1_data1	46.928120	15.0	scaling_rSTAT5A_rel;offset_rSTAT5A_rel	sd_rSTAT5A_rel	model1_data1_rSTAT5A_rel
37	rSTAT5A_rel	NaN	model1_data1	47.836575	20.0	scaling_rSTAT5A_rel;offset_rSTAT5A_rel	sd_rSTAT5A_rel	model1_data1_rSTAT5A_rel
38	rSTAT5A_rel	NaN	model1_data1	46.928727	30.0	scaling_rSTAT5A_rel;offset_rSTAT5A_rel	sd_rSTAT5A_rel	model1_data1_rSTAT5A_rel
39	rSTAT5A_rel	NaN	model1_data1	40.597753	40.0	scaling_rSTAT5A_rel;offset_rSTAT5A_rel	sd_rSTAT5A_rel	model1_data1_rSTAT5A_rel
40	rSTAT5A_rel	NaN	model1_data1	43.783664	50.0	scaling_rSTAT5A_rel;offset_rSTAT5A_rel	sd_rSTAT5A_rel	model1_data1_rSTAT5A_rel
41	rSTAT5A_rel	NaN	model1_data1	44.457388	60.0	scaling_rSTAT5A_rel;offset_rSTAT5A_rel	sd_rSTAT5A_rel	model1_data1_rSTAT5A_rel
42	rSTAT5A_rel	NaN	model1_data1	41.327159	80.0	scaling_rSTAT5A_rel;offset_rSTAT5A_rel	sd_rSTAT5A_rel	model1_data1_rSTAT5A_rel
43	rSTAT5A_rel	NaN	model1_data1	41.062733	100.0	scaling_rSTAT5A_rel;offset_rSTAT5A_rel	sd_rSTAT5A_rel	model1_data1_rSTAT5A_rel
44	rSTAT5A_rel	NaN	model1_data1	39.235830	120.0	scaling_rSTAT5A_rel;offset_rSTAT5A_rel	sd_rSTAT5A_rel	model1_data1_rSTAT5A_rel
45	rSTAT5A_rel	NaN	model1_data1	36.619461	160.0	scaling_rSTAT5A_rel;offset_rSTAT5A_rel	sd_rSTAT5A_rel	model1_data1_rSTAT5A_rel
46	rSTAT5A_rel	NaN	model1_data1	34.893714	200.0	scaling_rSTAT5A_rel;offset_rSTAT5A_rel	sd_rSTAT5A_rel	model1_data1_rSTAT5A_rel
47	rSTAT5A_rel	NaN	model1_data1	32.211077	240.0	scaling_rSTAT5A_rel;offset_rSTAT5A_rel	sd_rSTAT5A_rel	model1_data1_rSTAT5A_rel

Parameters to be optimized in the inner problem are specified via the PEtab parameter table by setting a value in the non-standard column parameterType (offset for offset parameters, scaling for scaling parameters, and sigma for sigma parameters). When using hierarchical optimization, the nine overriding parameters {offset,scaling,sd}_{pSTAT5A_rel,pSTAT5B_rel,rSTAT5A_rel} are to estimated in the inner problem.

[5]:

petab_problem_hierarchical.parameter_df

[5]:

	parameterName	parameterScale	lowerBound	upperBound	nominalValue	estimate	parameterType
parameterId
Epo_degradation_BaF3	EPO_{degradation,BaF3}	log10	0.00001	100000.0	0.026983	1	None
k_exp_hetero	k_{exp,hetero}	log10	0.00001	100000.0	0.000010	1	None
k_exp_homo	k_{exp,homo}	log10	0.00001	100000.0	0.006170	1	None
k_imp_hetero	k_{imp,hetero}	log10	0.00001	100000.0	0.016368	1	None
k_imp_homo	k_{imp,homo}	log10	0.00001	100000.0	97749.379402	1	None
k_phos	k_{phos}	log10	0.00001	100000.0	15766.507020	1	None
ratio	ratio	lin	0.00000	5.0	0.693000	0	None
sd_pSTAT5A_rel	\sigma_{pSTAT5A,rel}	lin	0.00000	inf	3.852612	1	sigma
sd_pSTAT5B_rel	\sigma_{pSTAT5B,rel}	lin	0.00000	inf	6.591478	1	sigma
sd_rSTAT5A_rel	\sigma_{rSTAT5A,rel}	lin	0.00000	inf	3.152713	1	sigma
specC17	specC17	lin	-5.00000	5.0	0.107000	0	None
offset_pSTAT5A_rel	NaN	lin	-100.00000	100.0	0.000000	1	offset
offset_pSTAT5B_rel	NaN	lin	-100.00000	100.0	0.000000	1	offset
offset_rSTAT5A_rel	NaN	lin	-100.00000	100.0	0.000000	1	offset
scaling_pSTAT5A_rel	NaN	lin	0.00001	100000.0	3.852612	1	scaling
scaling_pSTAT5B_rel	NaN	lin	0.00001	100000.0	6.591478	1	scaling
scaling_rSTAT5A_rel	NaN	lin	0.00001	100000.0	3.152713	1	scaling

[6]:

# Create a pypesto problem with hierarchical optimization (`problem`)
importer = PetabImporter(
    petab_problem_hierarchical,
    hierarchical=True,
    model_name="Boehm_JProteomeRes2014_hierarchical",
)
problem = importer.create_problem(verbose=False)
# set option to compute objective function gradients using adjoint sensitivity analysis
problem.objective.amici_solver.setSensitivityMethod(
    amici.SensitivityMethod.adjoint
)

# ... and create another pypesto problem without hierarchical optimization (`problem2`)
importer2 = PetabImporter(
    petab_problem,
    hierarchical=False,
    model_name="Boehm_JProteomeRes2014_hierarchical",
)
problem2 = importer2.create_problem(verbose=False)
problem2.objective.amici_solver.setSensitivityMethod(
    amici.SensitivityMethod.adjoint
)

# Options for multi-start optimization
minimize_kwargs = {
    # number of starts for multi-start optimization
    "n_starts": 3,
    # number of processes for parallel multi-start optimization
    "engine": pypesto.engine.MultiProcessEngine(n_procs=3),
    # raise in case of failures
    "options": OptimizeOptions(allow_failed_starts=False),
    # use the Fides optimizer
    "optimizer": pypesto.optimize.FidesOptimizer(
        verbose=0, hessian_update=fides.BFGS()
    ),
}
# Set the same starting points for the hierarchical and non-hierarchical problem
startpoints = pypesto.startpoint.latin_hypercube(
    n_starts=minimize_kwargs["n_starts"],
    lb=problem2.lb_full,
    ub=problem2.ub_full,
)
# for the hierarchical problem, we only specify the outer parameters
outer_indices = [problem2.x_names.index(x_id) for x_id in problem.x_names]
problem.set_x_guesses(startpoints[:, outer_indices])
problem2.set_x_guesses(startpoints)

Compiling amici model to folder /home/docs/checkouts/readthedocs.org/user_builds/pypesto/checkouts/stable/doc/example/amici_models/0.23.1/Boehm_JProteomeRes2014_hierarchical.

Hierarchical optimization using analytical or numerical inner solver

[7]:

# Run hierarchical optimization using NumericalInnerSolver
start_time = time.time()
problem.objective.calculator.inner_solver = NumericalInnerSolver(
    minimize_kwargs={"n_starts": 1}
)
result_num = pypesto.optimize.minimize(problem, **minimize_kwargs)
print(f"{result_num.optimize_result.get_for_key('fval')=}")
time_num = time.time() - start_time
print(f"{time_num=}")

result_num.optimize_result.get_for_key('fval')=[125.28673998436817, 130.99467076361685, 161.19213320044827]
time_num=8.448185443878174

[8]:

# Run hierarchical optimization using AnalyticalInnerSolver
start_time = time.time()
problem.objective.calculator.inner_solver = AnalyticalInnerSolver()
result_ana = pypesto.optimize.minimize(problem, **minimize_kwargs)
print(f"{result_ana.optimize_result.get_for_key('fval')=}")
time_ana = time.time() - start_time
print(f"{time_ana=}")

result_ana.optimize_result.get_for_key('fval')=[125.28673998436817, 130.99467076361685, 161.19213320044827]
time_ana=8.450279712677002

[9]:

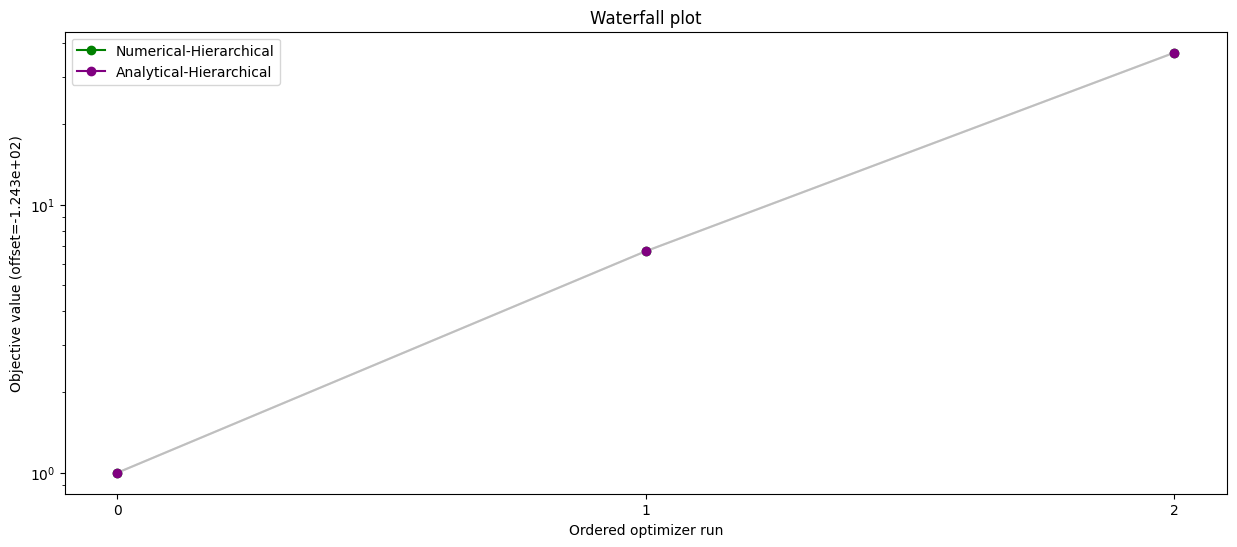
# Waterfall plot - analytical vs numerical inner solver
pypesto.visualize.waterfall(
    [result_num, result_ana],
    legends=["Numerical-Hierarchical", "Analytical-Hierarchical"],
    size=(15, 6),
    order_by_id=True,
    colors=np.array(list(map(to_rgba, ("green", "purple")))),
)

[9]:

<Axes: title={'center': 'Waterfall plot'}, xlabel='Ordered optimizer run', ylabel='Objective value (offset=-1.243e+02)'>

../_images/example_relative_data_16_1.png

[10]:

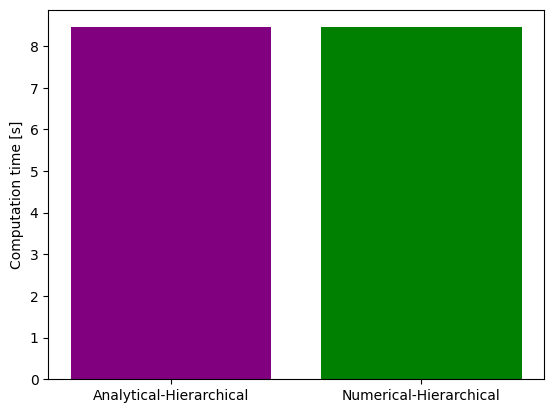
# Time comparison - analytical vs numerical inner solver
ax = plt.bar(x=[0, 1], height=[time_ana, time_num], color=["purple", "green"])
ax = plt.gca()
ax.set_xticks([0, 1])
ax.set_xticklabels(["Analytical-Hierarchical", "Numerical-Hierarchical"])
ax.set_ylabel("Computation time [s]")

[10]:

Text(0, 0.5, 'Computation time [s]')

../_images/example_relative_data_17_1.png

Comparison of hierarchical and non-hierarchical optimization

[11]:

# Run standard optimization
start_time = time.time()
result_ord = pypesto.optimize.minimize(problem2, **minimize_kwargs)
print(f"{result_ord.optimize_result.get_for_key('fval')=}")
time_ord = time.time() - start_time
print(f"{time_ord=}")

result_ord.optimize_result.get_for_key('fval')=[182.10084646572741, 314.8313572225626, 552.366118631411]
time_ord=45.82659196853638

[12]:

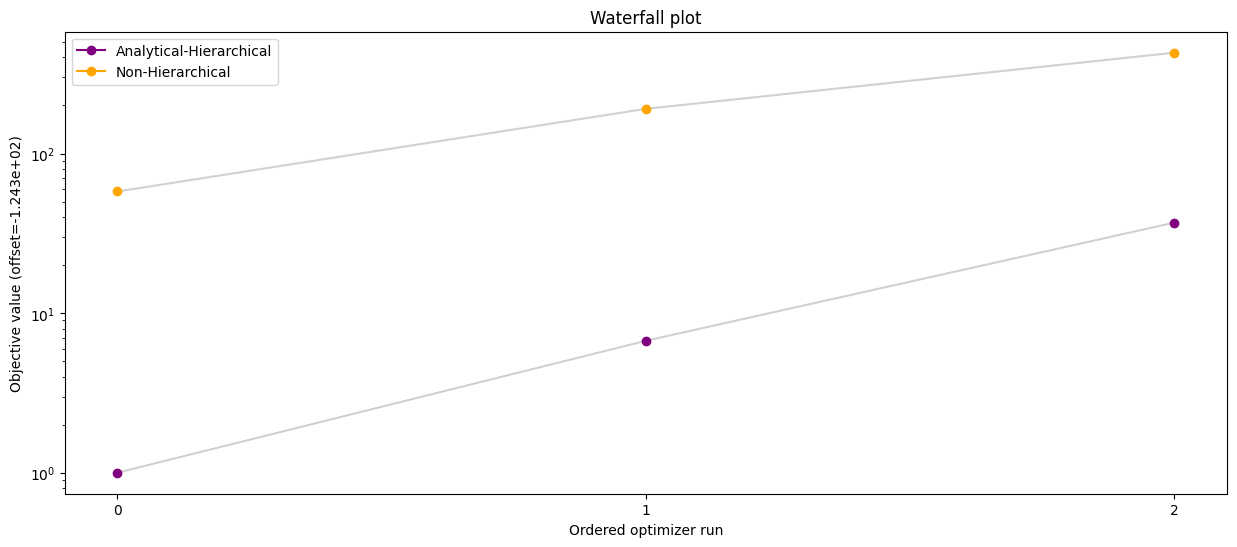
# Waterfall plot - hierarchical optimization with analytical inner solver vs standard optimization
pypesto.visualize.waterfall(
    [result_ana, result_ord],
    legends=["Analytical-Hierarchical", "Non-Hierarchical"],
    order_by_id=True,
    colors=np.array(list(map(to_rgba, ("purple", "orange")))),
    size=(15, 6),
)

[12]:

<Axes: title={'center': 'Waterfall plot'}, xlabel='Ordered optimizer run', ylabel='Objective value (offset=-1.243e+02)'>

../_images/example_relative_data_20_1.png

[13]:

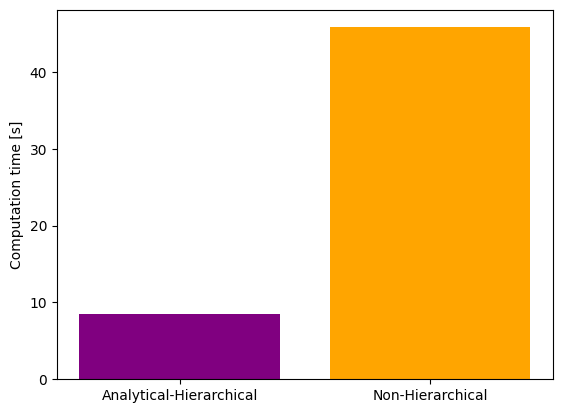
# Time comparison - hierarchical optimization with analytical inner solver vs standard optimization
import matplotlib.pyplot as plt

ax = plt.bar(x=[0, 1], height=[time_ana, time_ord], color=["purple", "orange"])
ax = plt.gca()
ax.set_xticks([0, 1])
ax.set_xticklabels(["Analytical-Hierarchical", "Non-Hierarchical"])
ax.set_ylabel("Computation time [s]")

[13]:

Text(0, 0.5, 'Computation time [s]')

../_images/example_relative_data_21_1.png

Comparison of hierarchical and non-hierarchical optimization with adjoint and forward sensitivities

[14]:

# Run hierarchical optimization with analytical inner solver and forward sensitivities
start_time = time.time()
problem.objective.calculator.inner_solver = AnalyticalInnerSolver()
problem.objective.amici_solver.setSensitivityMethod(
    amici.SensitivityMethod_forward
)
result_ana_fw = pypesto.optimize.minimize(problem, **minimize_kwargs)
print(f"{result_ana_fw.optimize_result.get_for_key('fval')=}")
time_ana_fw = time.time() - start_time
print(f"{time_ana_fw=}")

result_ana_fw.optimize_result.get_for_key('fval')=[125.28673785542964, 130.9946705087009, 161.19210128429035]
time_ana_fw=4.003589868545532

[15]:

# Waterfall plot - compare all scenarios
pypesto.visualize.waterfall(
    [result_ana, result_ana_fw, result_num, result_ord],
    legends=[
        "Analytical-Hierarchical (adjoint)",
        "Analytical-Hierarchical (forward)",
        "Numerical-Hierarchical",
        "Non-Hierarchical",
    ],
    colors=np.array(list(map(to_rgba, ("purple", "blue", "green", "orange")))),
    order_by_id=True,
    size=(15, 6),
)

[15]:

<Axes: title={'center': 'Waterfall plot'}, xlabel='Ordered optimizer run', ylabel='Objective value (offset=-1.243e+02)'>

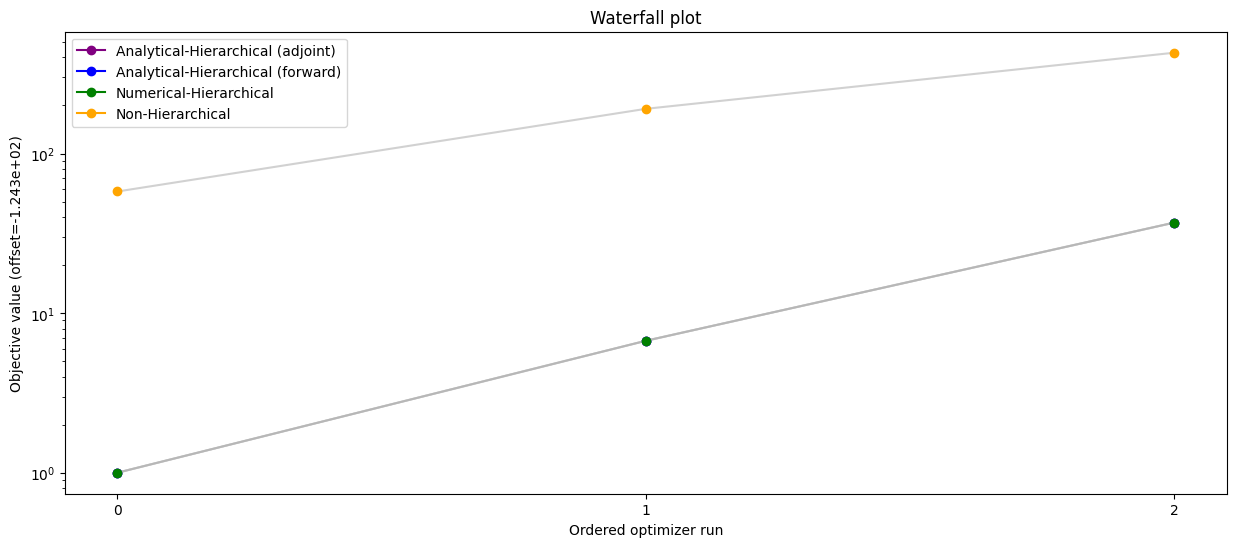
../_images/example_relative_data_24_1.png

[16]:

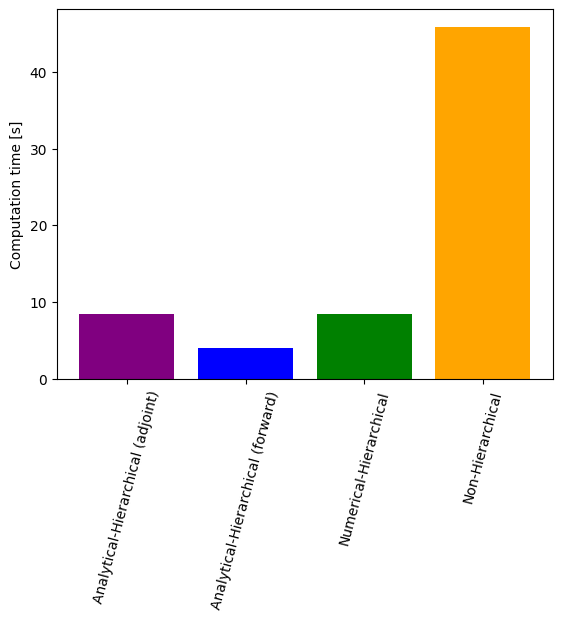
# Time comparison of all scenarios
import matplotlib.pyplot as plt

ax = plt.bar(
    x=[0, 1, 2, 3],
    height=[time_ana, time_ana_fw, time_num, time_ord],
    color=["purple", "blue", "green", "orange"],
)
ax = plt.gca()
ax.set_xticks([0, 1, 2, 3])
ax.set_xticklabels(
    [
        "Analytical-Hierarchical (adjoint)",
        "Analytical-Hierarchical (forward)",
        "Numerical-Hierarchical",
        "Non-Hierarchical",
    ]
)
plt.setp(ax.get_xticklabels(), fontsize=10, rotation=75)
ax.set_ylabel("Computation time [s]")

[16]:

Text(0, 0.5, 'Computation time [s]')

../_images/example_relative_data_25_1.png