Rosenbrock banana

Here, we perform optimization for the Rosenbrock banana function, which does not require an AMICI model. In particular, we try several ways of specifying derivative information.

import pypesto
import pypesto.visualize as visualize
import numpy as np
import scipy as sp
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D

%matplotlib inline

Define the objective and problem

# first type of objective
objective1 = pypesto.Objective(fun=sp.optimize.rosen,
                               grad=sp.optimize.rosen_der,
                               hess=sp.optimize.rosen_hess)

# second type of objective
def rosen2(x):
    return (sp.optimize.rosen(x),
            sp.optimize.rosen_der(x),
            sp.optimize.rosen_hess(x))
objective2 = pypesto.Objective(fun=rosen2, grad=True, hess=True)

dim_full = 10
lb = -5 * np.ones((dim_full, 1))
ub = 5 * np.ones((dim_full, 1))

problem1 = pypesto.Problem(objective=objective1, lb=lb, ub=ub)
problem2 = pypesto.Problem(objective=objective2, lb=lb, ub=ub)

Illustration

x = np.arange(-2, 2, 0.1)
y = np.arange(-2, 2, 0.1)
x, y = np.meshgrid(x, y)
z = np.zeros_like(x)
for j in range(0, x.shape[0]):
    for k in range(0, x.shape[1]):
        z[j,k] = objective1([x[j,k], y[j,k]], (0,))

fig = plt.figure()
fig.set_size_inches(*(14,10))
ax = plt.axes(projection='3d')
ax.plot_surface(X=x, Y=y, Z=z)
plt.xlabel('x axis')
plt.ylabel('y axis')
ax.set_title('cost function values')

Text(0.5, 0.92, 'cost function values')

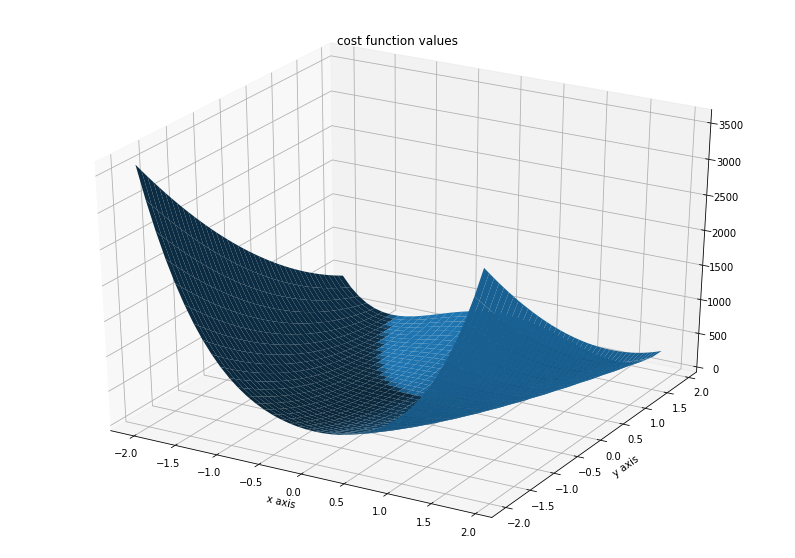
Run optimization

import pypesto.optimize as optimize

%%time

# create different optimizers
optimizer_bfgs = optimize.ScipyOptimizer(method='l-bfgs-b')
optimizer_tnc = optimize.ScipyOptimizer(method='TNC')
optimizer_dogleg = optimize.ScipyOptimizer(method='dogleg')

# set number of starts
n_starts = 20

# save optimizer trace
history_options = pypesto.HistoryOptions(trace_record=True)

# Run optimizaitons for different optimzers
result1_bfgs = optimize.minimize(
    problem=problem1, optimizer=optimizer_bfgs,
    n_starts=n_starts, history_options=history_options)
result1_tnc = optimize.minimize(
    problem=problem1, optimizer=optimizer_tnc,
    n_starts=n_starts, history_options=history_options)
result1_dogleg = optimize.minimize(
    problem=problem1, optimizer=optimizer_dogleg,
    n_starts=n_starts, history_options=history_options)

# Optimize second type of objective
result2 = optimize.minimize(
    problem=problem2, optimizer=optimizer_tnc, n_starts=n_starts)

Function values from history and optimizer do not match: 2.685929315976887, 2.9820162443657527
Parameters obtained from history and optimizer do not match: [ 9.81668828e-01  9.70664899e-01  9.44081691e-01  8.86185728e-01
  7.98866760e-01  6.27503392e-01  3.49193984e-01  1.00863999e-01
  1.18119992e-02 -4.83096174e-04], [0.98232811 0.9607169  0.93006041 0.86376905 0.72679074 0.51464422
 0.25715153 0.03390018 0.0134388  0.00224348]
Function values from history and optimizer do not match: 2.932320470464073, 3.104833804292291
Parameters obtained from history and optimizer do not match: [9.85695690e-01 9.66998320e-01 9.34405532e-01 8.72211105e-01
 7.61716907e-01 5.82160864e-01 2.90132686e-01 5.88015713e-02
 1.02493152e-02 1.44786818e-04], [9.76820249e-01 9.49203293e-01 9.03611145e-01 8.32711736e-01
 6.92021069e-01 4.71244784e-01 2.26981271e-01 1.93600745e-02
 9.06285841e-03 3.00716108e-04]
Function values from history and optimizer do not match: 7.128857018893593, 7.737539574292646
Parameters obtained from history and optimizer do not match: [-9.74521002e-01  9.48916364e-01  8.98382180e-01  7.95485807e-01
  6.32334509e-01  3.95389632e-01  1.55262583e-01  2.24615758e-02
  9.92812211e-03  4.70538835e-05], [-0.95137113  0.92287756  0.85600385  0.74220324  0.53469862  0.25223695
  0.05388462  0.01175751  0.01035533  0.00121333]
Function values from history and optimizer do not match: 4.047666500407507, 4.8092850089870245
Parameters obtained from history and optimizer do not match: [9.57097378e-01 9.15272882e-01 8.35583627e-01 6.92924153e-01
 4.69156347e-01 1.98916115e-01 2.87951418e-02 1.21495892e-02
 1.14276335e-02 2.48487865e-04], [9.37837181e-01 8.73541886e-01 7.61292462e-01 5.64720865e-01
 2.84119482e-01 6.17767487e-02 1.53662912e-02 1.54992154e-02
 1.49513982e-02 2.98560604e-04]
Function values from history and optimizer do not match: 4.760963749486806, 5.255690010134404
Parameters obtained from history and optimizer do not match: [-0.98990379  0.98886801  0.98189121  0.96587616  0.93451723  0.87262109
  0.75889559  0.56883791  0.31364781  0.07883034], [-0.99248035  0.99162316  0.97889433  0.95364865  0.91078502  0.8261375
  0.68236478  0.45820395  0.17444197  0.01383626]
Function values from history and optimizer do not match: 1.8159939922237558, 2.5425135960926237
Parameters obtained from history and optimizer do not match: [9.90583524e-01 9.80917081e-01 9.63072632e-01 9.30325108e-01
 8.61713989e-01 7.40678602e-01 5.38268550e-01 2.71328618e-01
 5.43996813e-02 7.89698144e-04], [9.89162276e-01 9.78043570e-01 9.51094059e-01 9.02211862e-01
 8.07645490e-01 6.35406055e-01 3.75384767e-01 1.11075371e-01
 1.30319964e-02 2.11963742e-04]
Function values from history and optimizer do not match: 2.2546577084566284, 2.988463828057193
Parameters obtained from history and optimizer do not match: [9.86890406e-01 9.73738159e-01 9.51089323e-01 9.02086672e-01
 8.09027663e-01 6.46629154e-01 4.04671023e-01 1.51442890e-01
 1.94187285e-02 2.45054194e-04], [9.81148194e-01 9.60640784e-01 9.21690034e-01 8.55030060e-01
 7.31180374e-01 5.23069013e-01 2.44624625e-01 3.39441804e-02
 1.03741576e-02 2.45306769e-05]
Function values from history and optimizer do not match: 0.3545683077008359, 0.5906121485206447
Parameters obtained from history and optimizer do not match: [0.99668472 0.99262575 0.98945665 0.98129911 0.96532923 0.93081497
 0.86315388 0.74328951 0.53910453 0.2736718 ], [0.9963228  0.99215562 0.98514259 0.97132273 0.94683482 0.89670025
 0.80300196 0.64224614 0.40061592 0.14210795]
Function values from history and optimizer do not match: 1.442951465698237, 2.117657844069939
Parameters obtained from history and optimizer do not match: [0.99253701 0.98698288 0.97438388 0.94864025 0.89249411 0.79343394
 0.62110958 0.37154848 0.12142293 0.00337751], [9.85576055e-01 9.72515609e-01 9.52500598e-01 9.14984751e-01
 8.40282960e-01 7.07108893e-01 4.93844010e-01 2.19299261e-01
 1.80684261e-02 2.39353088e-04]
Function values from history and optimizer do not match: 0.4310215367360306, 0.7200757805862191
Parameters obtained from history and optimizer do not match: [0.99728801 0.99265292 0.98655945 0.97724776 0.95330363 0.91375386
 0.83290125 0.68949822 0.4687524  0.21461214], [0.99666432 0.99530499 0.9871224  0.96976884 0.94230384 0.89383977
 0.79420195 0.62752848 0.3793222  0.11129682]
Function values from history and optimizer do not match: 6.33997905147026, 7.069668392692864
Parameters obtained from history and optimizer do not match: [7.84450616e-01 6.10188497e-01 3.64032562e-01 1.19476022e-01
 1.25200919e-02 9.74166479e-03 1.00503247e-02 8.51949533e-03
 9.92120699e-03 1.97235559e-04], [ 7.13358486e-01  4.93846146e-01  2.05601150e-01  2.46828697e-02
  1.00531820e-02  8.83759494e-03  9.93584452e-03  1.16356575e-02
  1.00772170e-02 -9.19777874e-05]
Function values from history and optimizer do not match: 1.080010188007246, 1.638996874292531
Parameters obtained from history and optimizer do not match: [0.99354151 0.98796198 0.97743947 0.96147507 0.92290179 0.84825176
 0.71159467 0.49318554 0.223647   0.03035961], [0.99093761 0.98310117 0.96952353 0.94165684 0.88399848 0.77718421
 0.59296742 0.3287277  0.08605952 0.00216266]
Function values from history and optimizer do not match: 6.334069745693479, 7.027921368861192
Parameters obtained from history and optimizer do not match: [-0.98264119  0.97390376  0.94694027  0.8905699   0.79188661  0.62198099
  0.37540054  0.12148722  0.01380672  0.00504649], [-0.97385408  0.95844934  0.9257917   0.85697013  0.71970238  0.49533252
  0.21270446  0.03011495  0.00979574 -0.00651404]

CPU times: user 2.74 s, sys: 37.7 ms, total: 2.78 s
Wall time: 2.74 s

Visualize and compare optimization results

# plot separated waterfalls
visualize.waterfall(result1_bfgs, size=(15,6))
visualize.waterfall(result1_tnc, size=(15,6))
visualize.waterfall(result1_dogleg, size=(15,6))

<matplotlib.axes._subplots.AxesSubplot at 0x7fb3be1ba0d0>

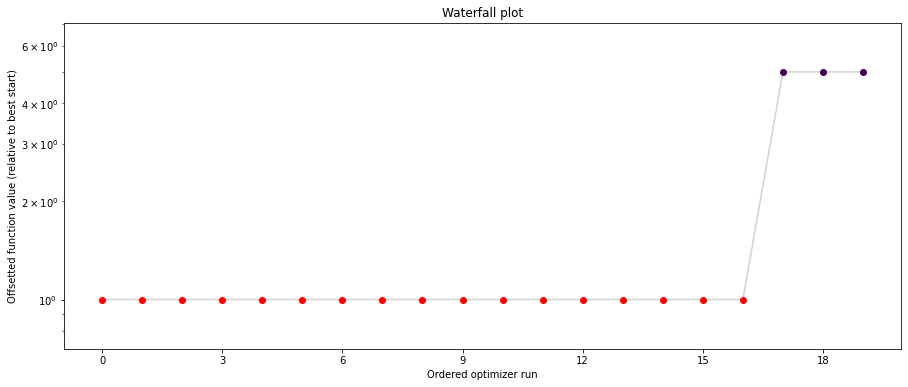
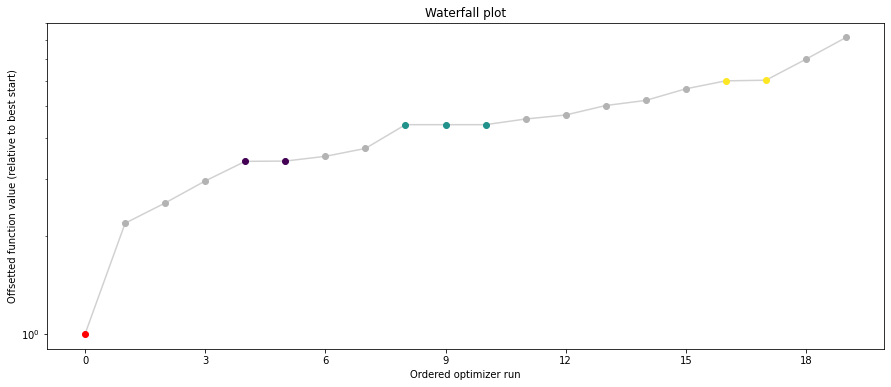
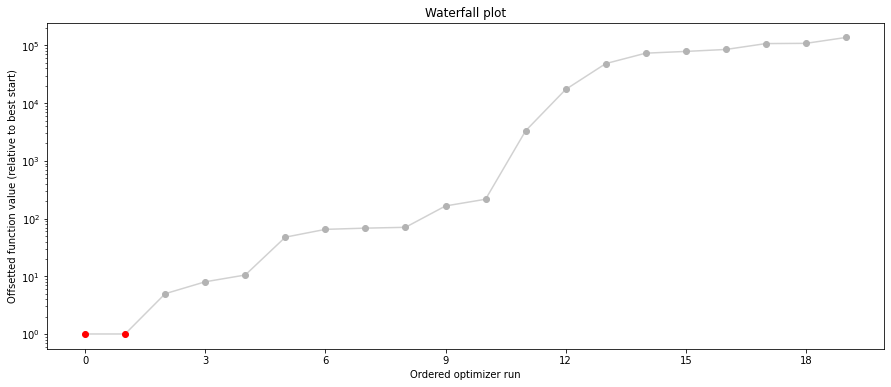
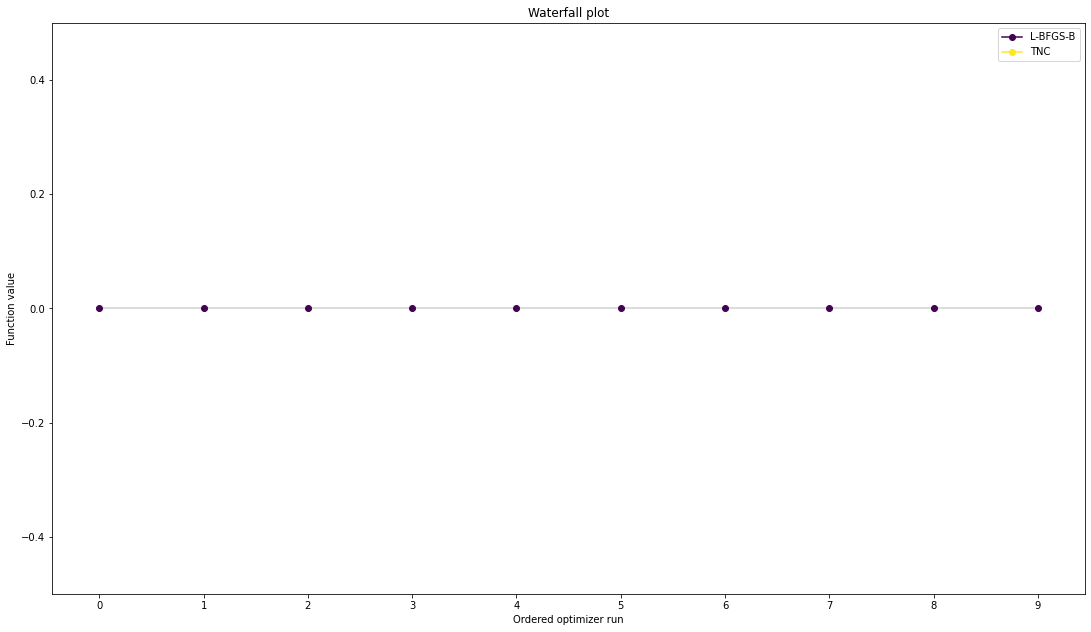
We can now have a closer look, which method perfomred better: Let’s first compare bfgs and TNC, since both methods gave good results. How does the fine convergence look like?

# plot one list of waterfalls
visualize.waterfall([result1_bfgs, result1_tnc],
                    legends=['L-BFGS-B', 'TNC'],
                    start_indices=10,
                    scale_y='lin')

<matplotlib.axes._subplots.AxesSubplot at 0x7fb3bf463760>

# retrieve second optimum
all_x = result1_bfgs.optimize_result.get_for_key('x')
all_fval = result1_bfgs.optimize_result.get_for_key('fval')
x = all_x[19]
fval = all_fval[19]
print('Second optimum at: ' + str(fval))

# create a reference point from it
ref = {'x': x, 'fval': fval, 'color': [
    0.2, 0.4, 1., 1.], 'legend': 'second optimum'}
ref = visualize.create_references(ref)

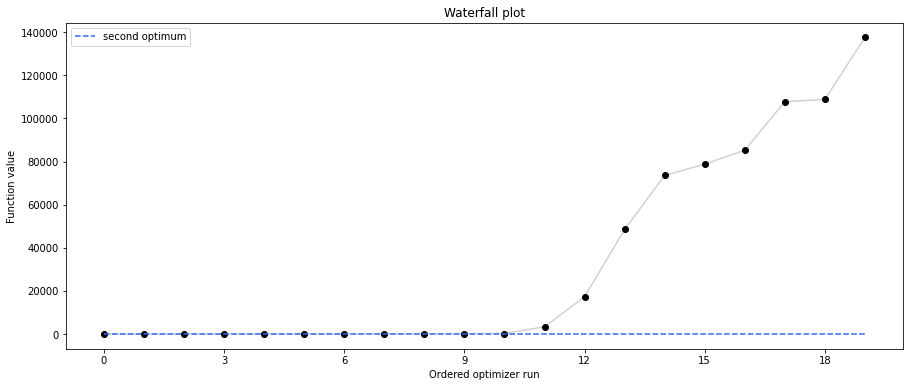
# new waterfall plot with reference point for second optimum
visualize.waterfall(result1_dogleg, size=(15,6),
                    scale_y='lin', y_limits=[-1, 101],
                    reference=ref, colors=[0., 0., 0., 1.])

Second optimum at: 3.9865791142048876

<matplotlib.axes._subplots.AxesSubplot at 0x7fb3bde83940>

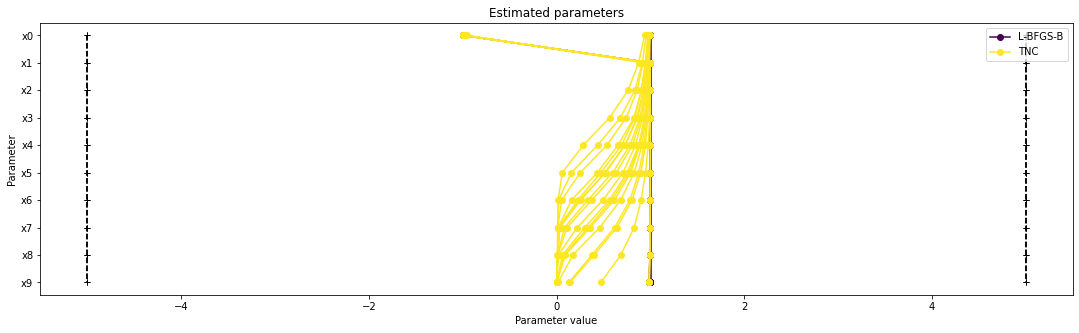
Visualize parameters

There seems to be a second local optimum. We want to see whether it was also found by the dogleg method

visualize.parameters([result1_bfgs, result1_tnc],
                     legends=['L-BFGS-B', 'TNC'],
                     balance_alpha=False)
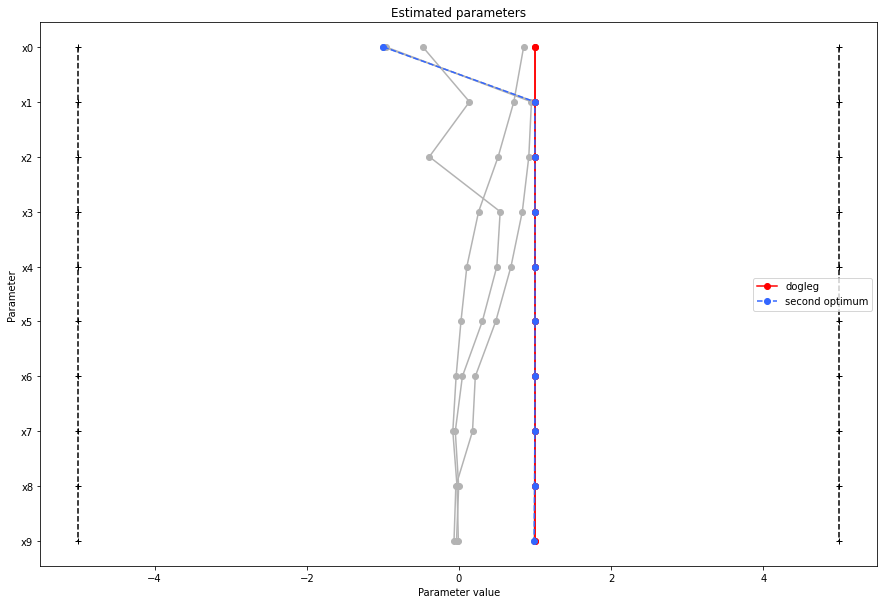
visualize.parameters(result1_dogleg,
                     legends='dogleg',
                     reference=ref,
                     size=(15,10),
                     start_indices=[0, 1, 2, 3, 4, 5],
                     balance_alpha=False)

<matplotlib.axes._subplots.AxesSubplot at 0x7fb3bdd5b430>

If the result needs to be examined in more detail, it can easily be exported as a pandas.DataFrame:

df = result1_tnc.optimize_result.as_dataframe(
    ['fval', 'n_fval', 'n_grad', 'n_hess', 'n_res', 'n_sres', 'time'])
df.head()

	fval	n_fval	n_grad	n_hess	n_res	n_sres	time
0	0.590612	101	101	0	0	0	0.052775
1	1.779748	101	101	0	0	0	0.049476
2	2.117658	101	101	0	0	0	0.039615
3	2.542514	101	101	0	0	0	0.064188
4	2.982016	101	101	0	0	0	0.024157

Optimizer history

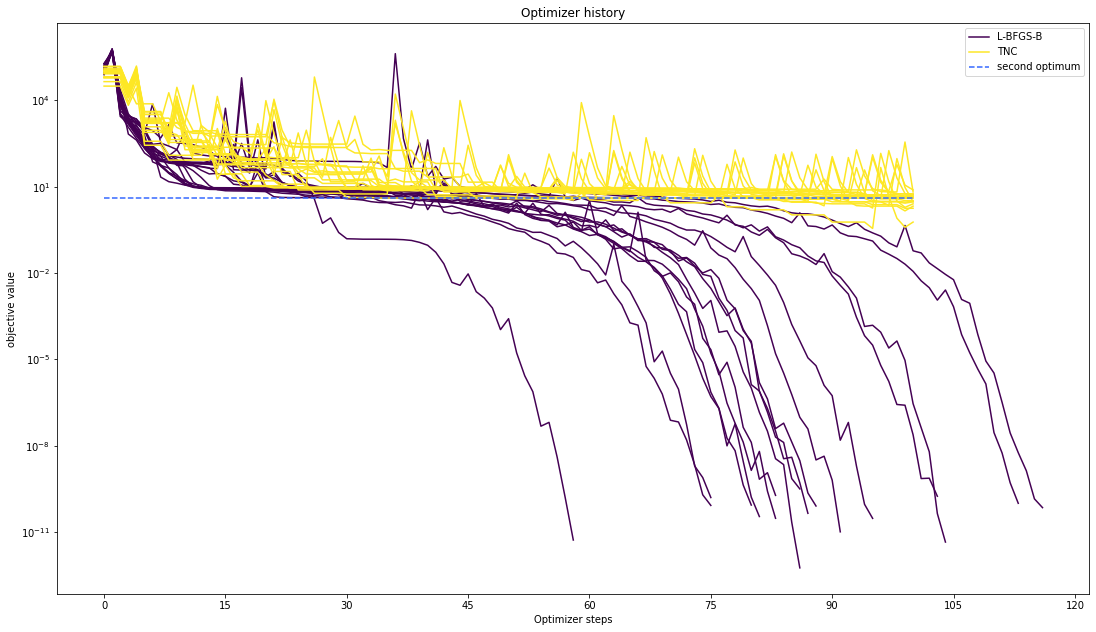
Let’s compare optimzer progress over time.

# plot one list of waterfalls
visualize.optimizer_history([result1_bfgs, result1_tnc],
                            legends=['L-BFGS-B', 'TNC'],
                            reference=ref)
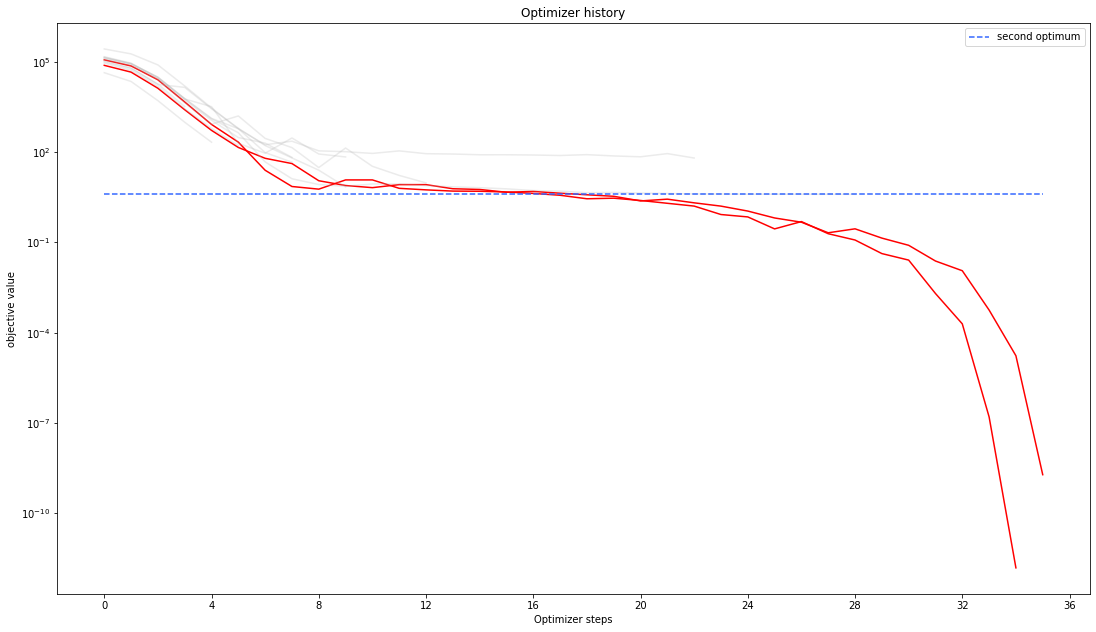
# plot one list of waterfalls
visualize.optimizer_history(result1_dogleg,
                            reference=ref)

<matplotlib.axes._subplots.AxesSubplot at 0x7fb3bdbcc820>

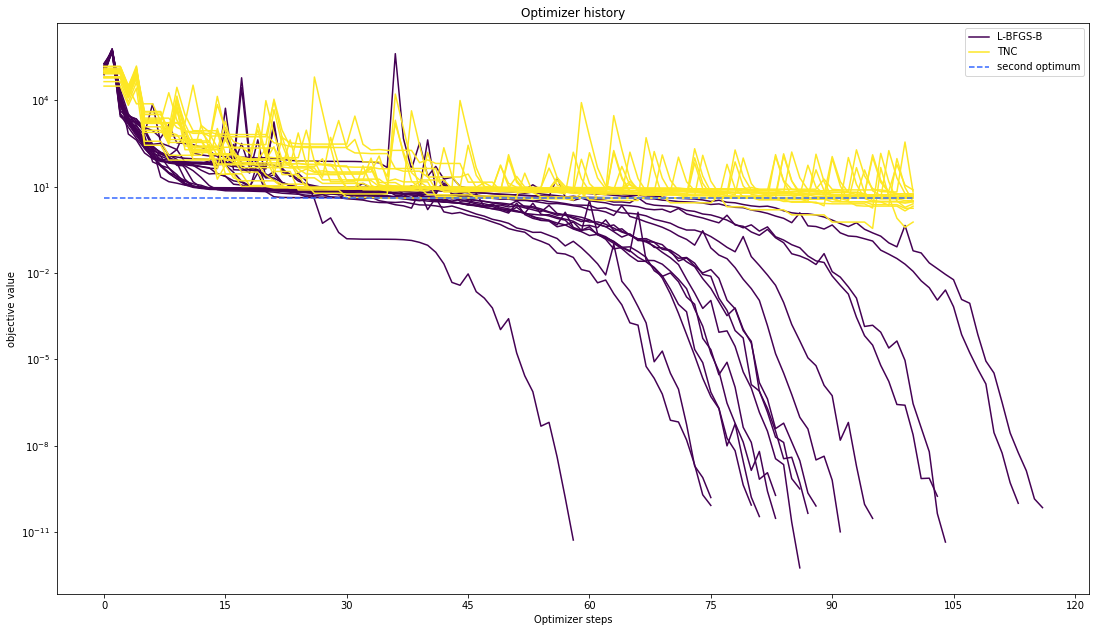
We can also visualize this usign other scalings or offsets…

# plot one list of waterfalls
visualize.optimizer_history([result1_bfgs, result1_tnc],
                            legends=['L-BFGS-B', 'TNC'],
                            reference=ref,
                            offset_y=0.)

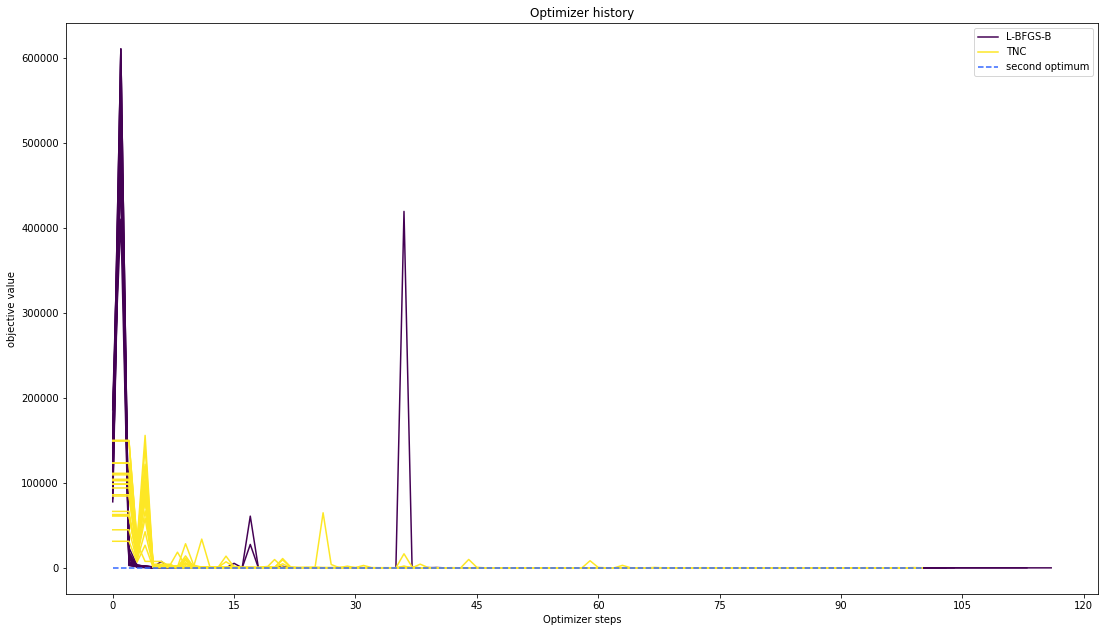
# plot one list of waterfalls
visualize.optimizer_history([result1_bfgs, result1_tnc],
                            legends=['L-BFGS-B', 'TNC'],
                            reference=ref,
                            scale_y='lin',
                            y_limits=[-1., 11.])

<matplotlib.axes._subplots.AxesSubplot at 0x7fb3be01d130>

Compute profiles

The profiling routine needs a problem, a results object and an optimizer.

Moreover it accepts an index of integer (profile_index), whether or not a profile should be computed.

Finally, an integer (result_index) can be passed, in order to specify the local optimum, from which profiling should be started.

import pypesto.profile as profile

%%time

# compute profiles
profile_options = profile.ProfileOptions(min_step_size=0.0005,
    delta_ratio_max=0.05,
    default_step_size=0.005,
    ratio_min=0.01)

result1_bfgs = profile.parameter_profile(
    problem=problem1,
    result=result1_bfgs,
    optimizer=optimizer_bfgs,
    profile_index=np.array([1, 1, 1, 0, 0, 1, 0, 1, 0, 0, 0]),
    result_index=0,
    profile_options=profile_options)

# compute profiles from second optimum
result1_bfgs = profile.parameter_profile(
    problem=problem1,
    result=result1_bfgs,
    optimizer=optimizer_bfgs,
    profile_index=np.array([1, 1, 1, 0, 0, 1, 0, 1, 0, 0, 0]),
    result_index=19,
    profile_options=profile_options)

CPU times: user 1.31 s, sys: 4.28 ms, total: 1.32 s
Wall time: 1.32 s

Visualize and analyze results

pypesto offers easy-to-use visualization routines:

# specify the parameters, for which profiles should be computed
ax = visualize.profiles(result1_bfgs, profile_indices = [0,1,2,5,7],
                        reference=ref, profile_list_ids=[0, 1])

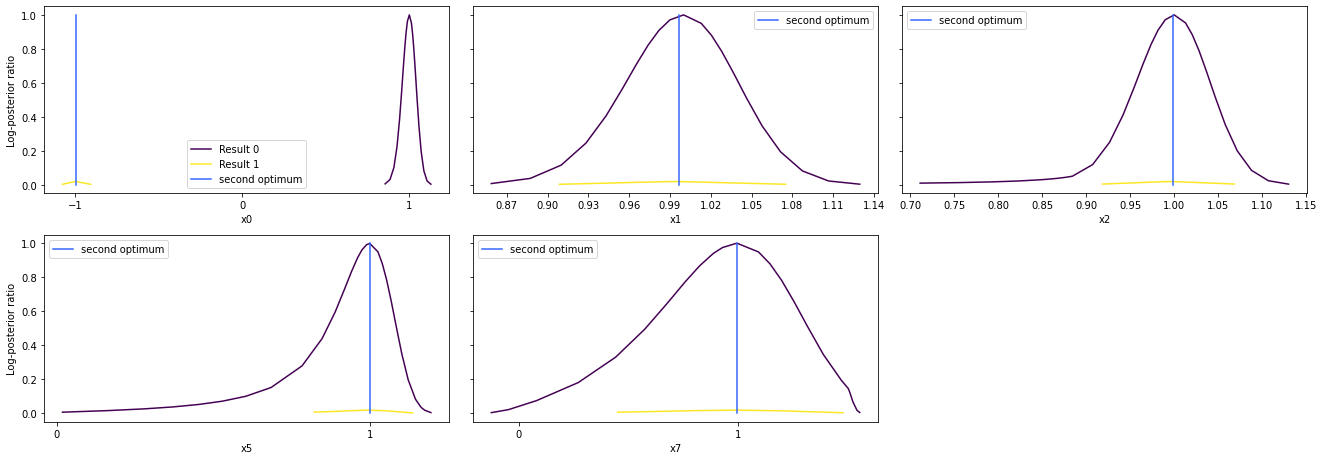
Approximate profiles

When computing the profiles is computationally too demanding, it is possible to employ to at least consider a normal approximation with covariance matrix given by the Hessian or FIM at the optimal parameters.

%%time

result1_tnc = profile.approximate_parameter_profile(
    problem=problem1,
    result=result1_bfgs,
    profile_index=np.array([1, 1, 1, 0, 0, 1, 0, 1, 0, 0, 0]),
    result_index=0,
    n_steps=1000)

CPU times: user 25 ms, sys: 16.3 ms, total: 41.4 ms
Wall time: 24.2 ms

These approximate profiles require at most one additional function evaluation, can however yield substantial approximation errors:

axes = visualize.profiles(
    result1_bfgs, profile_indices = [0,1,2,5,7], profile_list_ids=[0, 2],
    ratio_min=0.01, colors=[(1,0,0,1), (0,0,1,1)],
    legends=["Optimization-based profile", "Local profile approximation"])

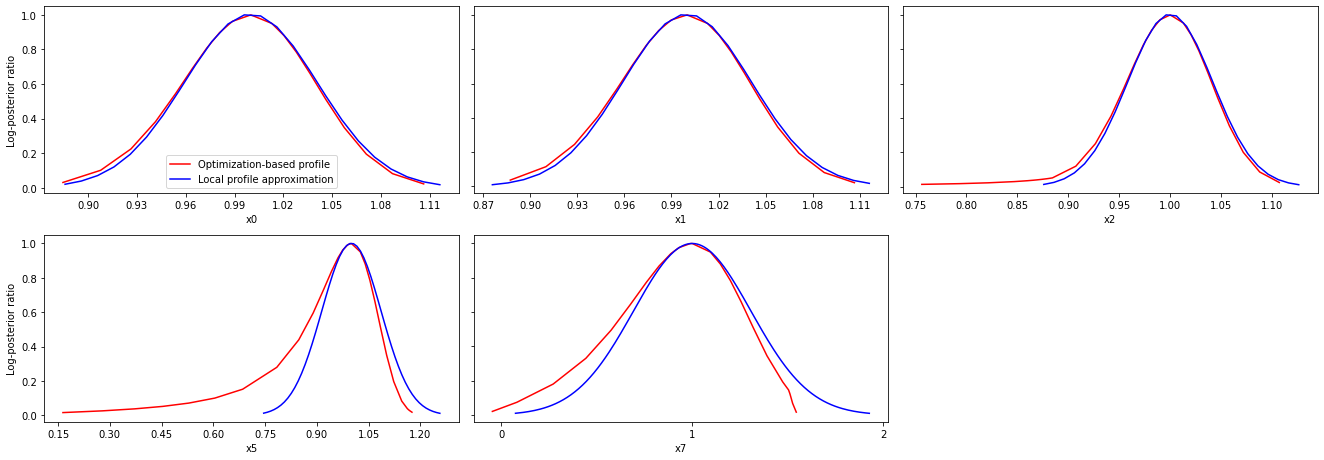
We can also plot approximate confidence intervals based on profiles:

visualize.profile_cis(
    result1_bfgs, confidence_level=0.95, profile_list=2)

<matplotlib.axes._subplots.AxesSubplot at 0x7fb3bda13f10>