Fixed parameters¶
In this notebook we will show how to use fixed parameters. Therefore, we employ our Rosenbrock example. We define two problems, where for the first problem all parameters are optimized, and for the second we fix some of them to specified values.
Define problem¶
[1]:
import pypesto
import pypesto.visualize
import numpy as np
import scipy as sp
import matplotlib.pyplot as plt
%matplotlib inline
[2]:
objective = pypesto.Objective(fun=sp.optimize.rosen,
grad=sp.optimize.rosen_der,
hess=sp.optimize.rosen_hess)
dim_full = 5
lb = -2 * np.ones((dim_full,1))
ub = 2 * np.ones((dim_full,1))
problem1 = pypesto.Problem(objective=objective, lb=lb, ub=ub)
x_fixed_indices = [1, 3]
x_fixed_vals = [1, 1]
problem2 = pypesto.Problem(objective=objective, lb=lb, ub=ub,
x_fixed_indices=x_fixed_indices,
x_fixed_vals=x_fixed_vals)
Optimize¶
[3]:
optimizer = pypesto.ScipyOptimizer()
n_starts = 10
result1 = pypesto.minimize(problem=problem1, optimizer=optimizer,
n_starts=n_starts)
result2 = pypesto.minimize(problem=problem2, optimizer=optimizer,
n_starts=n_starts)
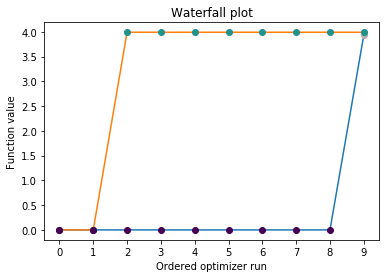
Visualize¶
[4]:
fig, ax = plt.subplots()
pypesto.visualize.waterfall(result1, ax)
pypesto.visualize.waterfall(result2, ax)
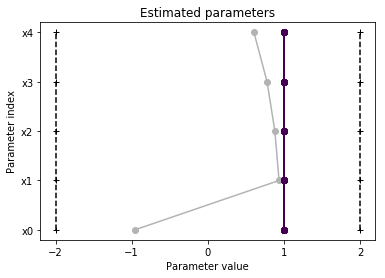
pypesto.visualize.parameters(result1)
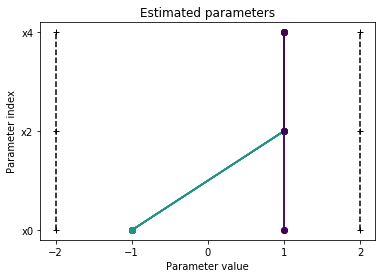
pypesto.visualize.parameters(result2)
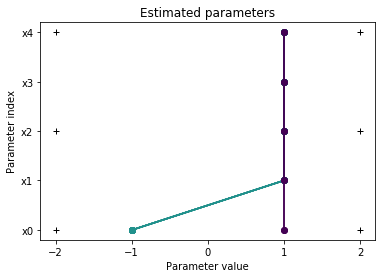
pypesto.visualize.parameters(result2, free_indices_only=False)
[4]:
<matplotlib.axes._subplots.AxesSubplot at 0x7f54c174de48>
[5]:
result1.optimize_result.as_dataframe(['fval', 'x', 'grad'])
[5]:
| fval | grad | x | |
|---|---|---|---|
| 0 | 6.647442e-15 | [-9.471566723124671e-07, 2.1021349555995795e-0... | [0.9999999965730911, 0.9999999954969394, 0.999... |
| 1 | 3.457526e-13 | [-5.2800846471136764e-06, -3.3572245747142896e... | [0.9999999337976915, 0.9999998804645882, 0.999... |
| 2 | 3.977885e-13 | [2.849416601133684e-06, -1.631494200631376e-05... | [1.0000000203239299, 1.0000000336259385, 1.000... |
| 3 | 5.131069e-13 | [-1.7633333620389112e-05, 2.2702306040974444e-... | [0.9999999656666152, 0.9999999752449003, 0.999... |
| 4 | 1.136030e-12 | [-5.235885777815437e-06, 2.0492304488450417e-0... | [0.9999999555620058, 0.9999999239915387, 0.999... |
| 5 | 1.408337e-12 | [1.907331444582324e-05, 2.095463179570122e-05,... | [0.9999999800522175, 0.9999999123214094, 0.999... |
| 6 | 2.901510e-11 | [5.880961607340145e-05, -0.0001001725246473881... | [0.9999996346096833, 0.9999991203684541, 0.999... |
| 7 | 1.178049e-10 | [0.00034230906294693863, -0.000134688339183694... | [1.0000006892941309, 1.0000005262631377, 1.000... |
| 8 | 3.892358e-10 | [-0.0003125535760549204, -0.000540050381524208... | [0.999999304112937, 0.9999993861314045, 1.0000... |
| 9 | 3.930839e+00 | [1.0349712058044247e-05, 3.916386398739036e-06... | [-0.9620510054878277, 0.9357393936941063, 0.88... |
[6]:
result2.optimize_result.as_dataframe(['fval', 'x', 'grad'])
[6]:
| fval | grad | x | |
|---|---|---|---|
| 0 | 1.848017e-13 | [1.161320144703573e-05, nan, 1.138211418469940... | [1.0000000144803007, 1.0, 1.0000000113593952, ... |
| 1 | 1.950306e-13 | [1.5797936376845116e-05, nan, 8.69990872045727... | [1.0000000196981744, 1.0, 1.0000000086825436, ... |
| 2 | 3.989975e+00 | [3.708520157630346e-08, nan, 8.708029498088168... | [-0.9949747467836382, 1.0, 1.0000000000869065,... |
| 3 | 3.989975e+00 | [-2.0752946916502424e-08, nan, 1.7918193731319... | [-0.9949747468568538, 1.0, 1.0000000001788243,... |
| 4 | 3.989975e+00 | [-7.013172895753428e-07, nan, 6.60039187652859... | [-0.9949747477183607, 1.0, 1.0000000006587217,... |
| 5 | 3.989975e+00 | [4.8148038946926874e-06, nan, 5.98716656044703... | [-0.994974740735661, 1.0, 1.000000005975216, 1... |
| 6 | 3.989975e+00 | [-3.6444866702289858e-06, nan, -1.258053682496... | [-0.9949747514440345, 1.0, 0.9999999874445739,... |
| 7 | 3.989975e+00 | [-1.9515809019488017e-05, nan, 2.2359531416176... | [-0.9949747715350857, 1.0, 1.000000022314901, ... |
| 8 | 3.989975e+00 | [-2.509148223639457e-05, nan, 1.94825262340907... | [-0.9949747785931701, 1.0, 1.0000000194436385,... |
| 9 | 3.989975e+00 | [3.7141079881841677e-05, nan, -2.5976819306825... | [-0.9949746998147513, 1.0, 0.9999999740750298,... |
[ ]: